Probability Axioms

After we finished the content of descriptive statistics, we moved on to the section of probability, which is really good at dealing with randomness. You have probably already come across some concepts of probability. In Lecture 4, we just made things formal. Probability axioms were introduced in this lecture. Those are the things we need to agree on. They are quite intuitive, and hopefully, you have no problem accepting them as facts:

  1. Nonnegativity: $\mathbb{P}(A) \geqslant 0$, for every event $A$
  2. Normalisation: $\mathbb{P}(\Omega) = 1$
  3. Additivity: If $A$ and $B$ are disjoint ($A \cap B = \varnothing$), then $$\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B)$$

A Recap of Set Notations

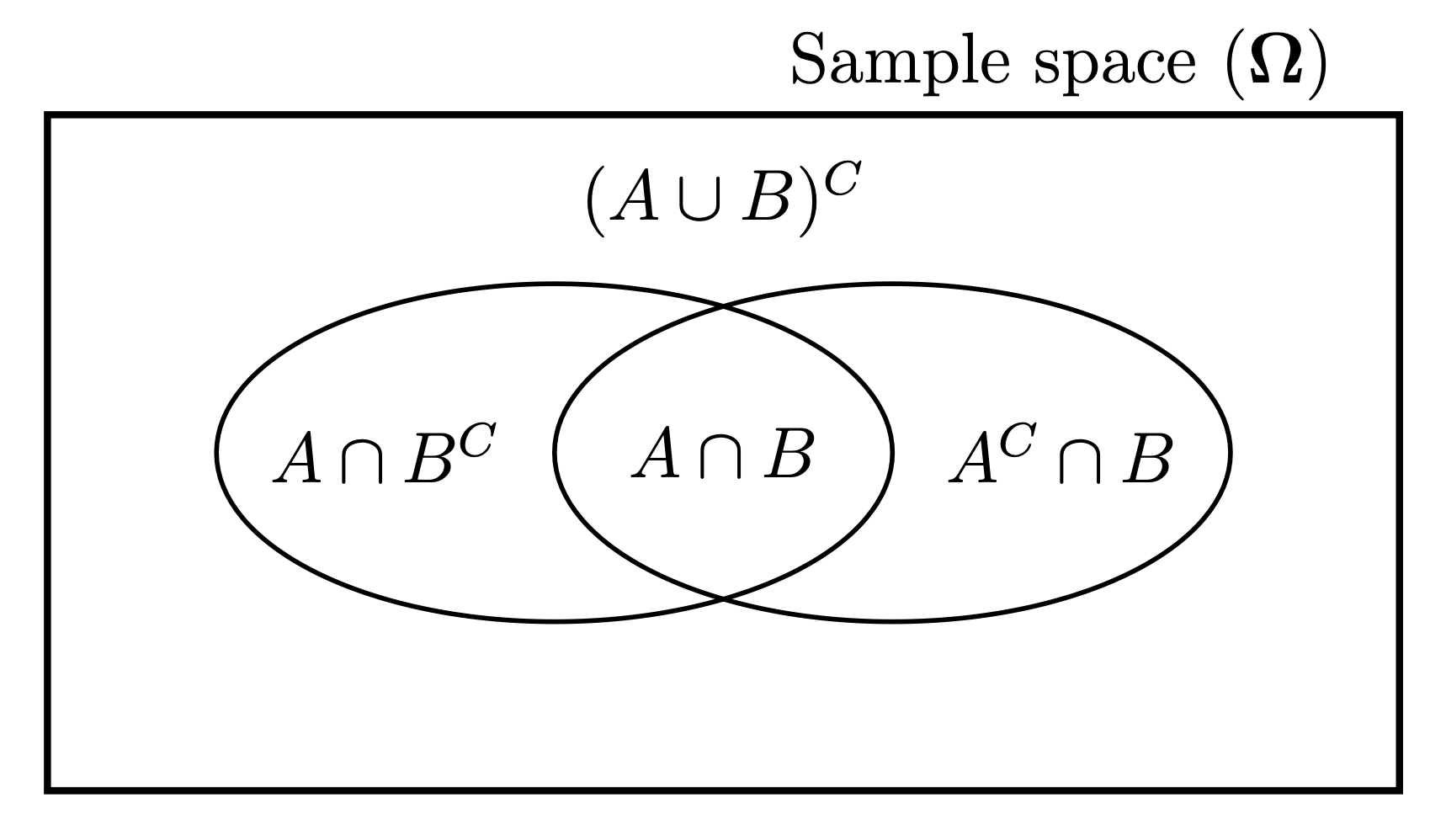
The sample space ($\Omega$) and probabilistic events ($A,B,C,\cdots$) are all expressed as sets, which can be written in the following two ways:

$$ \{s_1, s_2, s_3, \cdots \} \textmd{ or } \{s | s \textmd{ satisfies something} \} $$

The symbol | is read as “such that”. The complement of a set $S$ with respect to the sample space $\Omega$ is denoted by $S^C$. $A \cap B$ represents the common elements of sets $A$ and $B$:

$$ A \cap B = \{ x | x \in A \textmd{ and } x \in B \}$$

$A \cup B$ represents all the elements that are in either $A$ or $B$:

$$ A \cup B = \{ x | x \in A \textmd{ or } x \in B \}$$

$\varnothing$ is the empty set. In general, we visualise the relationship among different sets in Venn digrams:

Zero Probability

For most of the stuff we have talked about in this lecture, I think they follow our intuitions and we do not have a problem understanding them. One exception is the case when we have a continuos sample space. When we are dealing with a sample space with uncountably infinite outcomes, the probability of getting any specific outcome is zero. It has to be zero. Maybe I should say that we have to assign zero to any specific outcome, under the axioms we are using. It cannot be positive. Otherwise, using the additivity axiom, an event with a sufficiently large number of outcomes would have a probability of $>1$. When dealing with continuous or uncountable sample space, it makes more sense to work on intervals, which we will investigate more later.

For now, you can think that “probability of 0” does not necessarily mean “impossible”. To provide a rough example, consider the experiment in the lecture: we keep tossing a fair coin until the head appears for the first time and stop. Let the total number of tosses be $n$, the probability for some outcomes are:

$$ \begin{aligned} \mathbb{P}(H) &= \cfrac{1}{2}\\ \mathbb{P}(TH) &= \cfrac{1}{4}\\ \mathbb{P}(TTH) &= \cfrac{1}{8}\\ &\vdots \end{aligned} $$

The probability of any outcome would be $\cfrac{1}{2^n}$. Now let the event $A$ = { we keep getting tails and never stop }. We could calculate:

$$\mathbb{P}(A) = \lim_{n \to \infty}\cfrac{1}{2^n} $$

By definition, $\mathbb{P}(A) = 0$. Event $A$ is very unlikely to happen in real life, but theoretically, it is an event that could happen.

References