Lecture 8 introduced the concept of independence. It is a relatively straightforward concept to understand. Intuitively, events $A$ and $B$ are independent if:
$$\mathbb{P}(A|B)=\mathbb{P}(A), \mathbb{P}(B) \neq 0$$
Using Bayes’ terms, we can say that the posterior probability is equal to the prior probability. In other words, event $B$ has nothing to do with $A$; event $B$ does not provide any information about event $A$; given that event $B$ has occurred, we do not change our belief about event $A$ … Recall that from Lecture 5, we have:
$$\mathbb{P}(A|B)=\cfrac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \textmd{, } \mathbb{P}(B) \neq 0$$
If we move $\mathbb{P}(B)$ to the other side of the equation, and use our intuition about independence $\mathbb{P}(A|B) = \mathbb{P}(A)$, we get the mathematical definition of independence:
$$ \begin{aligned} A \textmd{ and } B &\textmd{ are independent if and only if:}\\ & \mathbb{P}(A \cap B) = \mathbb{P}(A)\mathbb{P}(B) \end{aligned} $$
The good thing about this definition is that it is easy to see $A$ and $B$ are symmetrical, and we do not really need to specify the ugly $\mathbb{P}(B) \neq 0$ in our intuitive definition.
Similarly, for a collection of events $A_1, A_2, …, A_n$, they are independent if and only if:
$$ \mathbb{P} \left( \bigcap_{i \in S} A_i \right) = \prod_{i \in S}\mathbb{P}(A_i), \textmd{ for every subset $S$ of } \{1,2, \cdots, n\} $$
During the lecture, we used many examples to showcase that the only way of checking if two events or a collection of events are independent or not is through the mathematical definition. In reality, people often use common sense, prior knowledge, intuition and experience to assume some events are independent. However, one needs to be very careful when doing so, as it might lead to wrong conclusions, which in certain situation can be catastrophic. We use the Sally Clark case to demonstrate this point.
When talking about conditional independence, we introduced a small quiz during the lecture:
It is known that the prevalence of a virus in the population is 0.5. We have a kit dedicated to detect this particular virus. The sensitivity of the kit is 0.9, and the specificity of the kit is 0.9 as well. Now a random person from the population gets tested by the kit, repeatedly. The first 3 tests all show positive results. What is the probability that the 4th test shows a positive result?
In general, always make a guess before you formally solve the problem. The process of guessing forces you to think about and get an intuition about the question. Sometimes, the intuition is more important and more difficult to come about. A correct intuition shows that you truly understand the question. In addition, once you get an answer by doing the formal calculation, you can always have a sanity check by comparing the calculated result to your intuitive guess. Doing this in a iterative way will help you learn.
Now let’s build up our intuition. Apparently, the test results are independent of each other if we know the person’s virus status (conditional independence). The probability of the 4th test being positive is basically 0.9 (if the person carries the virus) or 0.1 (if the person does not carry the virus). However, we do not know the person’s virus status. Therefore, before anything happens, we expect that the person has an equal chance of carrying or not carrying the virus. Now we observe that all 3 tests are positive, which is a new piece of information that can help us update our prior belief. We should take that information into account to calculate the probability of the next test (4th) being positive. We could think in this way: if the person does not carry the virus, the probability of observing 3 positive test results is $0.1^{3}$, which is quite small meaning it is kind of unlikely to happen. Yet, it happened! We see 3 positive test results, meaning that we are almost certain that the person carries the virus. If the person carries the virus, the probability of the 4th test being positive is 0.9. Therefore, our final answer should be very close to 0.9.
Is it? Let’s define $A=$ {the first 3 tests are positive} and $B=$ {the 4th test is positive} and build the following tree:
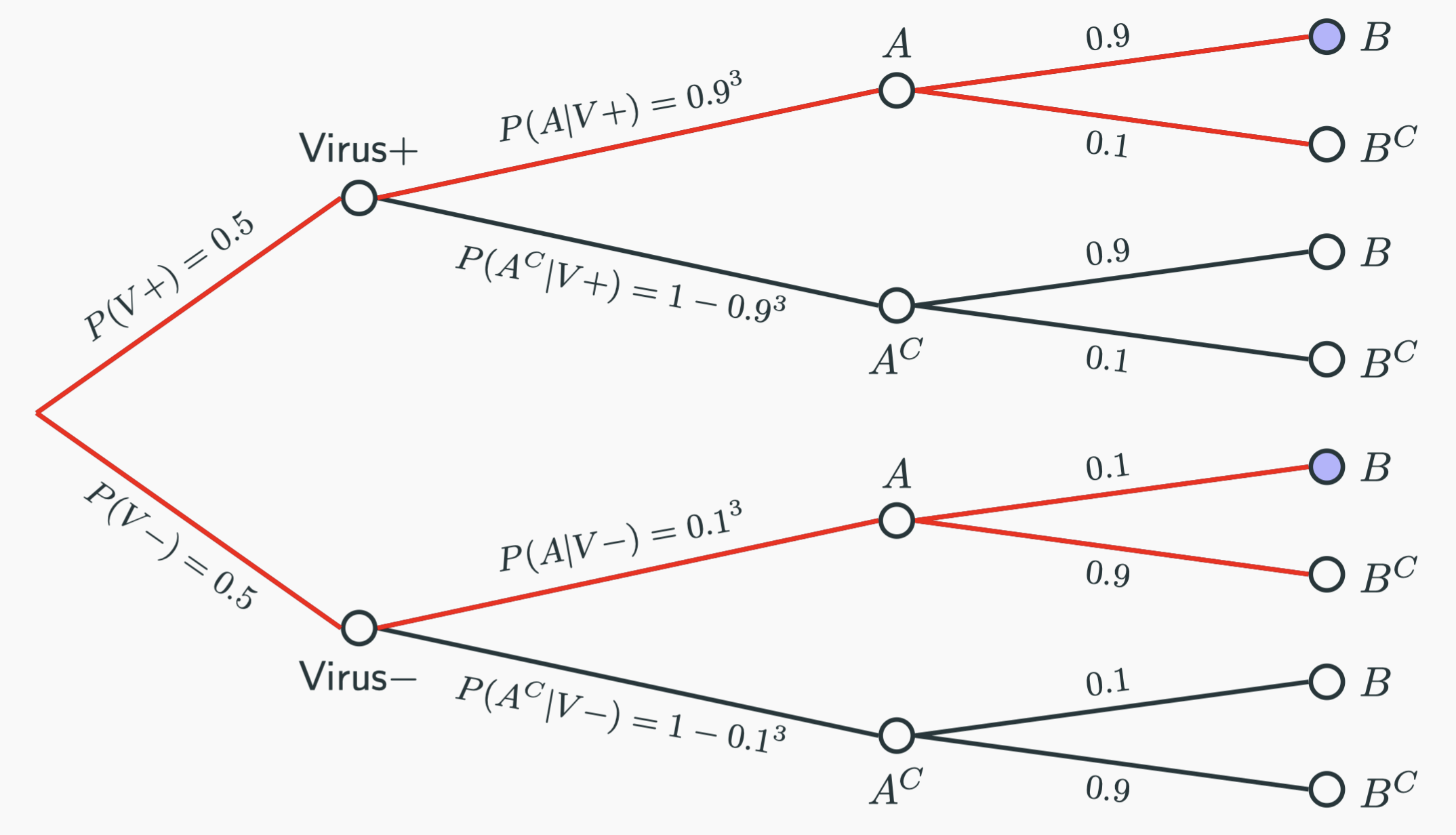
Since we know that $A$ has occurred, all of a sudden, we are living in a universe of the red branches. Our event of interest is basically the blue leaves. For each leaf, we could calculate the probability by the multiplication rule:
$$ \begin{aligned} \mathbb{P}(B|A) &= \cfrac{\textmd{Blue leaves}}{\textmd{Red branches}} \\[10pt] &= \cfrac{0.5 \times 0.9^{3} \times 0.9 + 0.5 \times 0.1^{3} \times 0.1}{0.5 \times 0.9^{3} + 0.5 \times 0.1^{3}}\\[10pt] & \approx 0.8989041095890411 \end{aligned} $$
The answer is very close to $0.9$, which is consistent with our intuition.