In Lecture 9, we paused a little bit and did a quick recap about the basic counting principles. The content was basically what you have learnt during your high school math classes but in English. You see that the counting principles we are talking about greatly help us calculate the probability of events consisting outcomes from discrete sample spaces.
You might ask why we bother to do a recap about counting. The discrete uniform law tells us that if we let all outcomes in a discrete sample space be equally likely, the probability of any event can be simply calculated as:
$$\mathbb{P}(A) = \cfrac{|A|}{|\Omega|}$$
$|A|$, $|\Omega|$ $\cdots$ represent the cardinality of a set, which is basically the number of elements in the set. Therefore, calculating the probability of an event comes down to counting the number of outcomes in the event and the total number of outcomes in the sample space.
The Basic Counting Principle
To help us count efficiently and systematically, we introduce a basic principle:
We divide a process into $r$ stages. There are $n_1$ possible choices in the first stage; for each possible choice from the first stage, there are $n_2$ possible choices; for each possible choice from the second stage, there are $n_3$ possible choices; $\cdots$; for each possible choice from the $(r-1)th$ stage, there are $n_r$ possible choices. If we could do that, the total number of choices we have is:
$$\prod_{i=1}^r n_i = n_1n_2n_3 \cdots n_r$$
You can put the following picture in your mind to help visualise this principle:
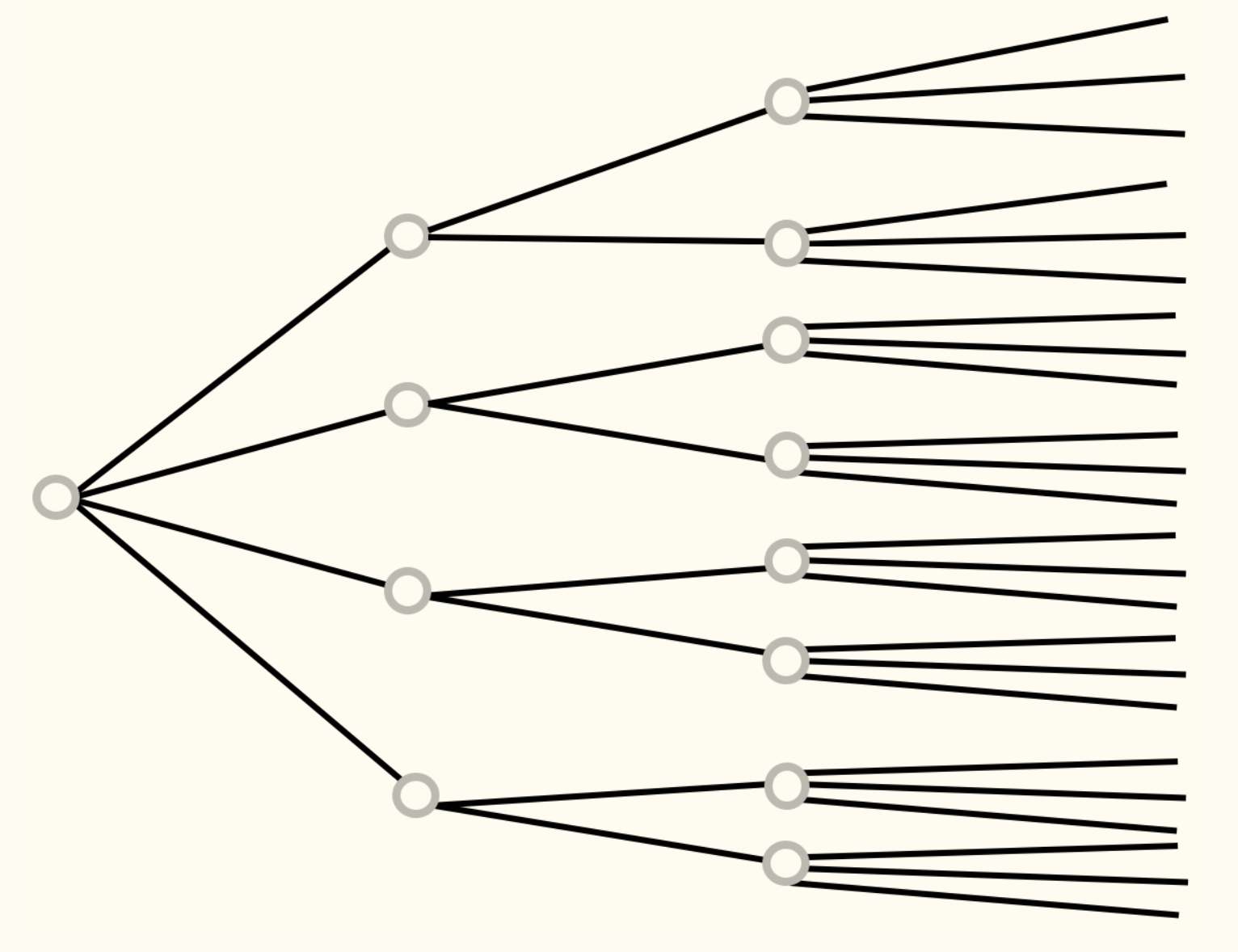
During the lecture, we used a few examples to practice using the basic principle. You have seen that most complicated counting problems can be easily broken down and use the above principle to count, meaning that the basic counting principle is all we need to know. However, it is still useful to know and memorise some common types of counting derived from the basic principle.
$k$-permutations
When we choose $k (k \leqslant n)$ objects from $n$ distinct objects and arrange them in a sequence, the total number of possible sequence, called $\boldsymbol{k}$-permutations, can be calculated by the basic counting principle:
$$n(n-1)(n-2) \cdots (n-k+1) = \cfrac{n(n-1)(n-2) \cdots 2 \cdot 1}{(n-k)\cdots 2 \cdot 1} = \cfrac{n!}{(n-k)!}$$
It is easy to see why the formula looks like that shown above. We can divide the problem into a $k$-stage counting process. In the first stage, we have $n$ choices; in the second stage, we are left with $n-1$ choices, etc. In the $k$th stage, we are left with $n-k+1$ choices. Therefore, based on the basic counting principle, the total number of choices is the product of them, which is exactly what is shown in the formula above.
In the special case where $k=n$, the number of total sequences is simply called permutations, which is basically $n!$.
Combinations
When we simply choose $k (k \leqslant n)$ objects from $n$ distinct objects without arranging them, meaning the order of the $k$ objects does not matter. This process is called combination. The number of choices is $C_n^k$. That is the notation you learnt in your high school math class. In this course, we use this notation:
$$\binom{n}{k}$$
It reads “n choose k”, which is exactly the same as $C_n^k$ but used more often. It is called the binomial coefficient. You all know from your high school that:
$$ \begin{aligned} \binom{n}{k} &= \cfrac{n(n-1)(n-2) \cdots (n-k+1)}{k!} \\[10pt] &= \cfrac{n(n-1)(n-2) \cdots (n-k+1) \cdot (n-k)(n-k-1) \cdots 2 \cdot 1}{k! \cdot (n-k)(n-k-1) \cdots 2 \cdot 1} \\[10pt] &= \cfrac{n!}{k!(n-k)!} \end{aligned} $$
and
$$ (a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^kb^{n-k} $$
Partitions
Actually, combination is a special case of partition. You can think of combination as partition an $n-$element set into two subsets, one with $k$ elements and the other $n-k$ elements. In a more general case, we want to partition an $n-$element set into $r$ disjoint subsets, with the first subset containing $n_1$ elements, the second $n_2$ elements, the third $n_3$ elements, etc. and finally the $r$th subset $n_r$ elements. Of course, it needs to satisfy that $n_1 + n_2 + \cdots + n_r = n$. How many ways can we do the partition as described?
We could divide this problem into an $r$-stage counting process. In the first stage, we choose $n_1$ elements for the first subset. Here we have $\binom{n}{n_1}$ choices. In the second stage, we are left with $n-n_1$ elements, and we choose $n_2$ elements for the second subset from those $n-n_1$ leftovers. Here we have $\binom{n-n_1}{n_2}$ choices. And so on … In the $r$th stage, we are left with $n-n_1 - \cdots - n_{r-1}$ elements, and we choose $n_r$ elements for the $r$th subset from those $n-n_1 - \cdots - n_{r-1}$ elements. Here, we have $\binom{n-n_1 - \cdots - n_{r-1}}{n_r}$ choices.
Using the basic counting principle, the total number of choices we have is basically the product of the number of choices at each stage:
$$\binom{n}{n_1} \cdot \binom{n-n_1}{n_2} \cdot \binom{n-n_1-n_2}{n_3} \cdots \binom{n-n_1-n_2- \cdots -n_{r-1}}{n_r}$$
If you expand each combination, you will find that it is equal to:
$$\cfrac{n!}{n_1!n_2! \cdots n_r!}$$
We denote the above as:
$$\binom{n}{n_1,n_2,\cdots,n_r}$$
It is called the multinomial coefficient.