Lecture 10 Random Variables

In this lecture, we introduced perhaps the first “new”¹ concept in this course: random variables. It is very important to understand the concepts of random variables and the expectation and variance of a random variable. When coming across something new, always start with something simple to get a rough idea. Therefore, we used some simple and intuitive examples, such as coin tossing, during the lectures.

Random Variables

A random variable is defined as a a real-valued function defined on a sample space $\Omega$. In a particular experiment, a random variable (r.v.) would be some function that assign a real-valued number to each possible outcome.

Recall the definition of a function back in your high school math class. When we talk about functions, we can think of them in two ways:

1. A function is like a machine with a set of defined rules. You input one thing. Then the machine returns a single output. The output is purely dependent on the input. If you put an apple in, and the machine returns a pear. Then the machine always returns a pear as long as the input is an apple. It does not matter whether you put an apple yesterday, today or tomorrow.
2. A function is a “mapping” or “association” of the elements from one set (say, $\boldsymbol{A}$) to the elements of another set (say, $\boldsymbol{B}$). Every element in $\boldsymbol{A}$ must have one and only one element in $\boldsymbol{B}$ associated with it.

I find both interpretations are useful in different scenarios. In the case of random variables, a random variable is basically a function that maps the outcome from the sample space to a real-valued number. That is: $\Omega \mapsto \mathbb{R}$.

We could use “tossing a coin three times” as an example. Again, do not think of this as three experiments. Instead, treat this example as a single experiment with three tosses. We only assess the final results after three tosses. It is easy to list every outcome in the sample space. We could define different random variables on the same sample space, depending on what we are interested in. For example, we could let the random variable $X$ be the number of tails. Or we could also define the random variable $Y$ as the number of heads. To visualise the random variables:

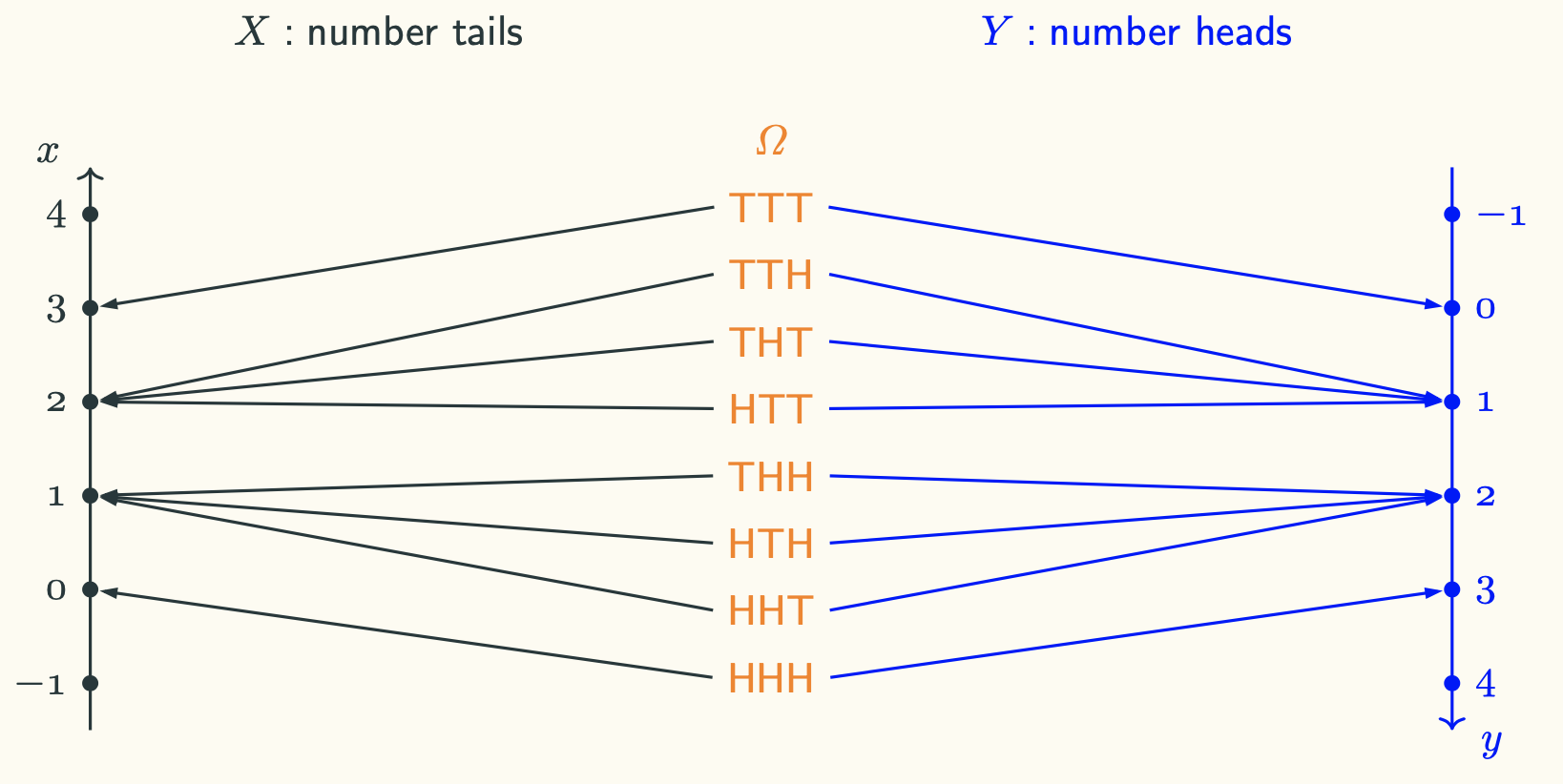
Why Introducing Random Variables?

Now you may ask: why? Why do we care about and introduce random variables? In many probabilistic models, the outcomes are numerical, or we could associate some numerical values to them. In future, we would like to gradually put the sample space at the background and directly work on the numbers and assign probabilities to the numbers, because sometimes it is not even clear what the sample space is. In addition, with the concept of random variables, we could talk about other useful things, such as expectation and variance.

Probability Mass Functions (PMFs)

Again, when we come across a new concept, we should always start with simple examples to get our intuition right. Based on the numbers that a random variable can take, we have discrete or continuous random variables. The discrete case is simpler than the continuous one. Therefore, let’s first talk about discrete random variables.

In general, we use the capital latin letter $X,Y,Z, \cdots$ to represent the random variable itself and use the lower-case latin letter $x,y,z,\cdots$ to represent the real-valued number that the random variable can take. Using the previous example, apparently the random variables $X$ and $Y$ have different chances of taking different values $x$ and $y$, respectively. For discrete random variables, we would describe the probability of them taking different values. To this end, we use probability mass function, or PMF. You can think of it as a table with every single possible value that the random variable can take together with the probability of taking the value. In terms of the random variable $X$ in the previous example of “tossing a coin three times”:

$x$	$\mathbb{P}(X=x)$
$0$	$\frac{1}{8}$
$1$	$\frac{3}{8}$
$2$	$\frac{3}{8}$
$3$	$\frac{1}{8}$

More formally we write a PMF like this:

$$ p_X(x) = \begin{cases} \cfrac{1}{8} & \textmd{, when } x=0 \textmd{ or } 3\\[10pt] \cfrac{3}{8} & \textmd{, when } x=1 \textmd{ or } 2\\[10pt] 0 & \textmd{, otherwise} \end{cases} $$

The small $p$ stands for PMF. The subscript capital $X$ is telling us the PMF is with respect to the random variable $X$. The small $x$ in the parentheses is the real-valued number taken by the random variable $X$. This is how we interpret the PMF $p_{X}(x)$:

$$p_X(x) = \mathbb{P}(\{ X=x \}) = \mathbb{P}(\{ \omega \in \Omega | X(\omega) = x \})$$

With the introduction of random variables and PMFs, we can now talk about the average and dispersion of a random variable, which will be very useful in terms of modelling probabilistic events.

Expectation

The expectation (also called the expected value or the mean) of a random variable can be thought as some sort of average number that the random variable takes after repeating the experiment for a large number of times. For examples, the random variable $X$ can take the values $x_1, x_2, x_3, \cdots, x_r$, each with a probability of $p_X(x_1), p_X(x_2), p_X(x_3), \cdots, p_X(x_r)$, respectively. If I keep repeating the experiment for $N$ times, the number of times $X$ takes the specific value $x_i$ is $n_i$. Then the average of $X$ is:

$$\cfrac{x_1n_1 + x_2n_2 + \cdots x_rn_r}{n_1 + n_2 + \cdots + n_r} = \cfrac{n_1}{N} \cdot x_1 + \cfrac{n_2}{N} \cdot x_2 + \cdots + \cfrac{n_r}{N} \cdot x_r$$

If we interpret probability as relative frequency and $N$ is really large, we believe that $\frac{n_i}{N} \approx p_X(x_i)$. Now recall what we have learnt from Lecture 3, the above average is essentially a weighted average of all the possible values of $X$.

Therefore, we denote the expectation of $X$ as $\mathbb{E}[X]$, and it is calculated by:

$$\mathbb{E}[X] = \sum_{x} xp_X(x)$$

Some useful properties of the expectation include:

1. $\mathbb{E}[g(X)] = \sum\limits_{x}g(x)p_X(x)$
2. $\mathbb{E}[a X + b] = a \mathbb{E}[{X}] + b$, where $a, b$ are constants

The proof can be found in the Extra Reading Material from this lecture.

Variance & Standard Deviation

The variance of $X$, denoted by $\mathbb{V}\textmd{ar}(X)$, is defined as:

$$\mathbb{V}\textmd{ar}(X) = \mathbb{E}\left[ \left( X - \mathbb{E}[X] \right)^2 \right]$$

The standard deviation of $X$, denoted by $\sigma_X$, is defined as:

$$\sigma_X = \sqrt{\mathbb{V}\textmd{ar}(X)}$$

Before we look at the meaning of variance, let’s analyse the expression first. $X$ is a random variable, and $\mathbb{E}[X]$ is a value. Then $(X - \mathbb{E}[X])^2$ is a function of the random variable $X$, which is also a random variable. Therefore, it is reasonable to ask what the expectation of $(X - \mathbb{E}[X])^2$ is. That is what the formula about.

By taking a closer look, we see that the random variable $(X - \mathbb{E}[X])^2$ is basically the squared distance between a random variable and its mean. It is a measurement of the dispersion of a random variable, which you can relate to what we have talked about in Lecture 3. The standard deviation is basically the square root of the variance, which has the same unit with the original random variable.

Some useful properties of the variance include:

1. $\mathbb{V}\textmd{ar}(X) = \mathbb{E}[X^2] - (\mathbb{E}[{X}])^2$
2. $\mathbb{V}\textmd{ar}(aX) = a^2\mathbb{V}\textmd{ar}(X)$

The proof can be found in the Extra Reading Material from this lecture.