Once we have seen some discrete random variables, we can move on to look at continuous random variables. As the name indicated, the numbers taken by a continuous random variable are continuous. Like we discussed before, in this case the probability of taking any specific number is zero. Therefore, it does NOT make sense to use PMF to describe a continuous random variable. Instead, we use probability density function (PDF), denoted by $f_X(x)$.
Probability Density Functions (PDFs)
A PDF similar to a PMF that it still takes a number that the random variable can take and return a new number. However, unlike PMF, the number returned by a PDF is the probability density, NOT the probability. Probability densities satisfy:
$$\mathbb{P}(x \in B) = \int_{B}f_{X}(x)\,\mathrm{d}x$$
for every subset $B$ of the real line. And:
$$\mathbb{P}(a \leqslant X \leqslant b) = \int_{a}^{b}f_{X}(x)\,\mathrm{d}x$$
for any interval on a real line.
When dealing with continuous random variables, it does not make sense to talk about each specific number. We talk about intervals. We use PDF such that the area under the curve of an interval represents the probability of the random variable falling into that interval.
Having said that, now if I put a number $x$ into $f_X(x)$, I still get a number returned by the PDF. You tell me that the number is not the probability. What is it? How should I interpret this probability density? One way of looking at densities is to think about a very small interval $\delta$, and put the following picture in your head:
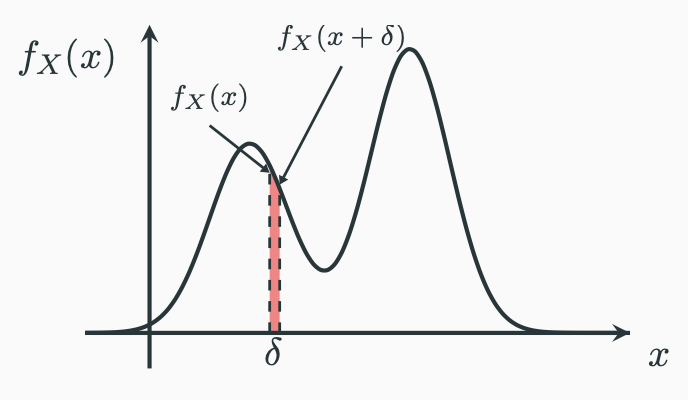
Since $\delta$ is vary small we have:
$$\mathbb{P}(x \leqslant X \leqslant x+\delta) = \int_{x}^{x+\delta}f_X(x)\,\mathrm{d}x = f_X(x)\cdot \delta$$
It means that the probability of the random variable falling into a very small interval is basically the probability density multiplied by the length of the small interval. Alternatively, you can move the small interval to the other side of the equation:
$$f_X(x) = \cfrac{\mathbb{P}(x \leqslant X \leqslant x+\delta)}{\delta}$$
It shows that we could interpret the probability density as the probability per unit length.
Comparisons To Discrete Random Variables
Since we have introduced discrete random variables, there is not really anything new in terms of continuous random variables. For the things related to discrete random variables, we also have them for continuous random variables, such as expectations and variances. When having trouble dealing with a concept in the continuous case, think of its counterpart in the discrete case. When we do summation in the discrete case, we do integration in the continuous case:
| The continuous case | The discrete case |
|---|---|
| $\mathbb{E}[X] = \int_{-\infty}^{\infty}xf_X(x)\,\mathrm{d}x$ | $\mathbb{E}[X] = \sum_{x}xp_X(x)$ |
| $\mathbb{E}[g(X)] = \int_{-\infty}^{\infty}g(x)f_X(x)\,\mathrm{d}x$ | $\mathbb{E}[g(X)] = \sum_{x}g(x)p_X(x)$ |
| $\mathbb{V}\textmd{ar}(X) = \int_{-\infty}^{\infty}\left(X-\mathbb{E}[X]\right)^2f_X(x)\,\mathrm{d}x$ | $\mathbb{V}\textmd{ar}(X)= \sum_{x}\left( X - \mathbb{E}[X] \right)^2p_X(x)$ |
Cumulative Density Functions (CDFs)
To help calculate probabilities in a convenient way, we can look at the cumulative density function (CDF) of a continuous random variable. It is denoted and defined as:
$$F_X(x) = \mathbb{P}(X \leqslant x) = \int_{-\infty}^{x}f_X(t)\,\mathrm{d}t$$
It is easy to see that:
$$\mathbb{P}(a \leqslant X \leqslant b) = \int_{a}^{b}f_X(x)\,\mathrm{d}x = F_X(b) - F_X(a)$$
Therefore, the CDF is the original function of the PDF, and the PDF is basically the derivate of the CDF:
$$f_X(x) = F^{\prime}_X(x)$$
Normal (Gaussian) Random Variables
Perhaps one of the most important continuous random variables is normal or Gaussian random variables. The PDF of a normal random variable is:
$$f_X(x)=\cfrac{1}{\sqrt{2\pi}\sigma}\,e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
When the normal random variables were introduced to me in school, the above PDF was just thrown to us. We then started to use it for various things. I have always been wondering where exactly it comes from, how to derive that PDF and why $e$ and $\pi$ are there. If you do some internet search, you will find some articles about how to derive the normal PDF. Many of them (for example, this one), use the “dart throwing” example and introduce polar coordinates to eventually get the famous PDF shown above. It is indeed a beautiful calculus practice. However, the example is not really intuitive. It is not so obvious why the “dart throwing” thought experiment is done in the first place and how it is related to the normal PDF.
Apparently, more context is needed. I think the most intuitive way of introducing the normal PDF is just follow the history. We have the following two ways of deriving the normal PDF … roughly …
1. As An Approximation Tool
In late 1600s and early 1700s, some mathematicians were working on gambling-related problems. They used binomial distributions a lot. Calculating the binomial coefficients was difficult, apparently, due to the complexity of factorials. They wanted to have some sort of approximation to avoid the calculation of factorials. The French mathematician Abraham de Moivre started working on that in 1721. In 1733, using an factorial approximation (today known as the Stirling’s Formula), he found out that when $n$ is large the probabilities around the central terms of the binomial distribution with $p=\frac{1}{2}$ can be approximated by:
$$\binom{n}{\frac{n}{2}+d}\left(\cfrac{1}{2}\right)^n \approx \cfrac{2}{\sqrt{2\pi n}}\,e^{-\frac{2d^2}{n}}$$
Later on, the French mathematician Pierre-Simon Laplace extended it to a more general case, and eventually led to the De Moivre–Laplace Theorem:
$$\binom{n}{k}p^k q^{n-k} \approx \cfrac{1}{\sqrt{2\pi npq}}\,e^{-\frac{(k-np)^2}{2npq}} \textmd{ , where } p+q=1,p,q > 0$$
which you may recognise as very similar to the normal PDF. The proof of the above theorem can be found in this Wikipedia page. In order to understand the proof, you need to know Stirling’s formula:
$$n! \approx \sqrt{2\pi n} \left( \cfrac{n}{e} \right)^n $$
In addition, you also need to be familiar with the following Taylor expansion:
$$\ln(1+x) = \sum_{n=1}^{\infty}(-1)^{n+1}\cfrac{x^n}{n} = x - \cfrac{x^2}{2} + \cfrac{x^3}{3} - \cfrac{x^4}{4} + \cdots $$
That’s all you need to know. The rest are basically algebraic manipulation, and you just have to be patient. Try it yourself!
2. The Error Curve
Back in the days, many astronomers were trying to measure and predict the trajectories and positions of different “heavenly bodies”. They were well aware that their measurements had errors, that is, the difference between the real location and the measurement. People were interested in finding a function to describe the error. The legendary Carl Friedrich Gauss was one of them. In his seminal work Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections), Gauss was trying to find the function to describe the error. Based on some assumptions that were supported by experience and data accumulated previously, he was abel to get the following PDF describing the error:
$$f_X(x) = \cfrac{h}{\sqrt{\pi}}\,e^{-h^2x^2}$$
which is kind of a prototype of the standard normal PDF that is used today. Of course, the above formula is a modernised version. Gauss’ original writing was:
$$\varphi\Delta=\cfrac{h}{\sqrt{\pi}}\,e^{-hh\Delta\Delta}$$
Gauss also commented on $h$:
Finally, the constant $h$ can be considered as the measure of precision of the observations.
The exact procedures to get to that point and the final form of the normal PDF that is commonly seen in modern text books deserves an entire post on its own on another day. I will probably write about it in future when I have time and fully digested the section in Gauss’ book. We will make an attempt to partly reproduce Gauss’ procedure in Lecture 18. For now, check those articles in the References section for more details.
The French mathematician Pierre-Simon Laplace was also searching for the error PDF but ended up with a weird one. However, it is his Central Limit Theorem that makes the normal PDF so useful. Anyway, we will dedicate an entire lecture (Lecture 13) in the next lesson to talk about normal PDFs. You will see why and how it is useful.
About The Word “Distribution”
I know that we have used the word “distribution”, even though we have not really define what exactly do we mean by “distribution”. In the Descriptive Statistics section, it is a histogram of the data you have. Now that we know the concept of random variables, the word “distribution” essentially means the PMF or the PDF of the random variable. When we say “a random variable $X$ follows a binomial (or normal) distribution”, we mean the PMF (or PDF) of $X$ is a binomial PMF (or a normal PDF).
Parameters of A Distribution
If you pay attention to the titles of each sections in this post, you will notice that all of them are in plural forms, such as random variables, PMFs and PDFs. Why? When we talk about binomial random variables, there are many of them. When we talk about normal random variables, there are many of them as well. What are the differences? They have different parameters.
The parameters describe the shape and some characteristics of the distribution. Once the random variable takes a value, you need the parameters to get the probability or density. For example, if $X$ is a binomial random variable and we want to calculate $\mathbb{P}(X=2)$, we need $n$ and $p$ for the calculation. Therefore, $n$ and $p$ are the parameters of binomial random variables. Similarly, if $Y$ is a normal random variable and we want to get the probability density at $Y=0$, we need $\mu$ and $\sigma^2$. Therefore, $\mu$ and $\sigma^2$ (some use $\sigma$) are the parameters of normal random variables.
When we say $X$ follows a certain distribution, we use the the following notation:
$$X \sim \textmd{Distribution short name (list of parameters)}$$
Here are some examples:
| Distribution | Notation |
|---|---|
| Bernoulli | $X \sim Ber(p)$ |
| Binomial | $X \sim B(n,p)$ |
| Poisson | $X \sim Pois(\lambda)$ |
| Normal | $X \sim \mathcal{N}(\mu, \sigma^2)$ |
- Normal distribution
- The Evolution of the Normal Distribution
- More on the history related to the normal distribution (in Chinese):