In this lecture, we introduced the most important two concepts in this entire course: the sampling distribution and the central limit theorem. We have seen how they help us make inferences about the population based on just one sample with limited size ($n$). They are the foundation for the hypothesis testing that we are going to introduce in the future.
Like mentioned before, in inferential statistics we would like to use the data from the sample to make inferences about certain unknown properties of the population. In this lesson, we are still going to assume that we know the population properties to see how the sample behaves. Soon we are going to do the opposite, I promise.
Three Distributions
One key thing from this lesson is to get clear ideas about three distributions and when to use each of them.
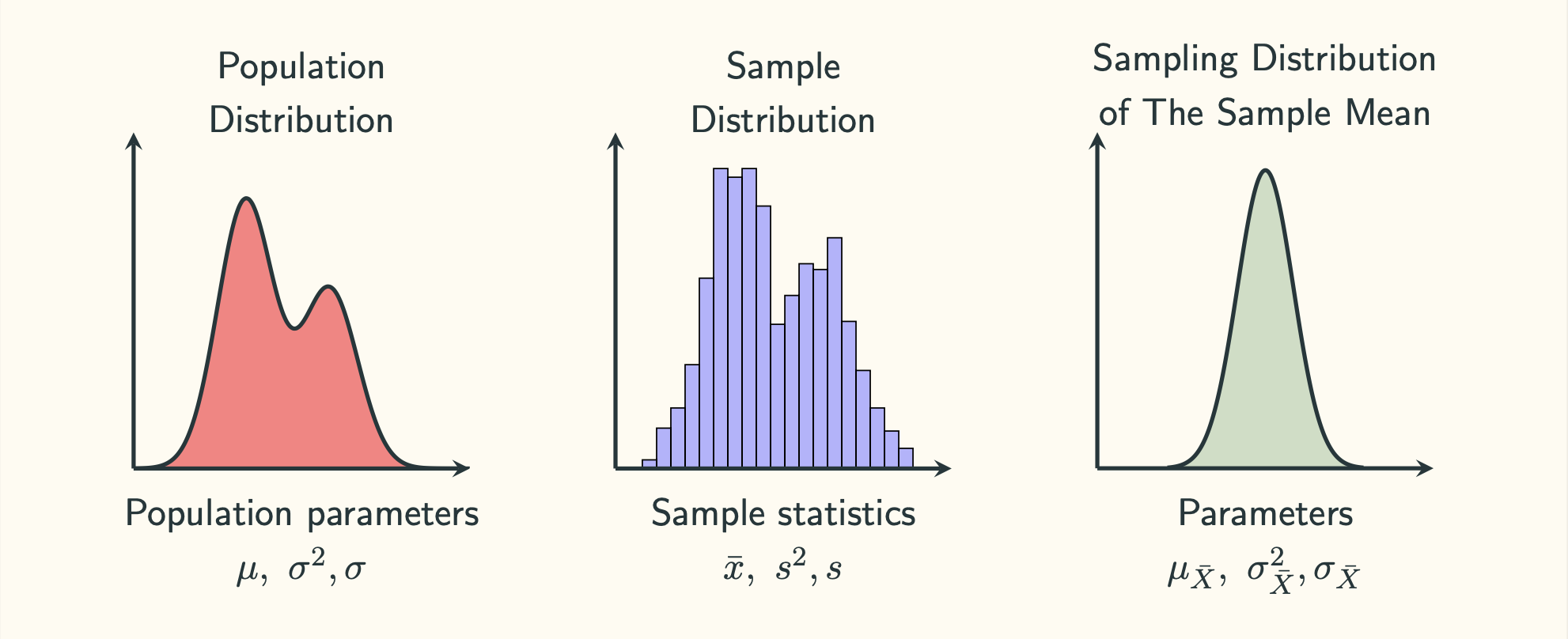
Population Distribution
Like the name suggests, the population distribution describes the behaviour of the population. Sometimes, we can think of the population as the sample space. A more useful thought is to treat the population as some sort of abstract concept that we are interested in. For example, if we are interested in the height of all human beings, our population can be an abstract concept of all people in the world. We could let the random variable $X$ represents the human height in centimetre. The random variable $X$ takes an individual (outcome) from the population (sample space) and returns an real-valued number representing the height. The distribution of $X$ is basically the population distribution.
If we know the distribution of $X$, we could nicely use the things we have learnt during the probability section to make some conclusions or predictions about an individual or a group of individuals from the population. In this lesson, we are going to assume that we know the distribution of $X$. However, we never really know the true distribution of $X$ in reality.
Sample Distribution
Recall what we have gone through during the lecture, the best way of thinking about a sample of size $n$ is to treat them as $n$ random variables ($X_1, X_2, \cdots, X_{n-1}, X_n$) randomly and independently chosen from the population. Since $X_1, X_2, \cdots, X_{n-1}, X_n$ come from the same population, they have identical distributions, all of which are the same as $X$, the population distribution. Therefore, we say that a sample of size $n$ from a population consists of $n$ independent and identically distributed (i.i.d.) random variables.
When we take a sample of size $n$, we get $n$ numbers. We can draw a histogram (or the like) with those $n$ numbers. The histogram (or the like) is the sample distribution. Like we discussed before, we do not really care about the exact values in the sample. We know that those values are only associated with this specific sample, and they are guaranteed to change when a new sample is drawn. Similarly, most of the time we do not really care about the sample distribution, either. However, remember that a sample is a micro-version of the population. It is a representation of the population. Therefore, the shape of the sample distribution tells us a lot about the shape of the population, especially when $n$ is large. Obtaining some ideas about the shape of the population distribution can be helpful in many cases. Therefore, the first thing we do when we get a sample is to draw and look at the sample distribution.
Sampling Distribution
This is probably one of the most important, if not the most important, concept in our course. When we get a sample with size $n$, we can use the following instructions to get some sample statistic:
$$\bar{X}=\cfrac{1}{n}\sum_{i=1}^{n} \textmd{ and } S^2=\cfrac{1}{n-1}\sum_{i=1}^{n}(X-\bar{X})^2$$
Apparently, $\bar{X}$ and $S^2$ are also random variables.
Now we draw a random sample with size $n$ from the population, and we observe the sample mean ($\bar{x}$) and sample variance ($s^2$) of this sample. Then we independently draw another sample with the same size ($n$) from the same population, we get another sample mean and sample variance. We keep repeating the sampling procedures for many times, we will get a lot of sample means and variances. On paper, we could do this forever. The distributions of those values, $\bar{x}$ and $s^2$, are basically the distributions of $\bar{X}$ and $S^2$, respectively. The distribution of $\bar{X}$ is called the sampling distribution of the sample mean. Similarly, the distribution of $S^2$ is called the sampling distribution of the sample variance.
Why do we care about the distribution of $\bar{X}$ and $S^2$? Well … consider the following scenario using the mean as an example. In a population where the population mean is 25, we draw a random sample (say, $n=10$) from it and observe the sample mean is 20. Now we are interested in this question: what is the probability of observing a sample ($\boldsymbol{n=10}$) with the sample mean equal to 20 or more extreme? Let’s call this question Question Q. Again, you may ask why? Why should we care about the answer to Question Q? Well … in a few lectures you will see why we are interested in Question Q and how the answer to it can provide us some knowledge about the population.
How do we solve it? We could treat probability as relative frequency in repeated experiments. Therefore, what we can do is to draw a sample ($n=10$) from the population, calculate and record the sample mean. Then we draw another sample ($n=10$) under the same condition from the same population, calculate and record the sample mean. We could keep doing this for a large number of times (say, $10,000$ or $100,000$ or more), so we would end up with many sample means. Finally, we check what fraction of those means are equal to or more than 20. That is basically the answer to Question Q. In reality, it is not practical to do the repeated sampling procedure. However, if we know the distribution of $\bar{X}$, Question Q can be easier answered using the property of $\bar{X}$. That’s how we use the sampling distribution.
The following slide summarises the three distributions we talked about:
The Central Limit Theorem
In order to answer Question Q, we need to figure out the distribution of $X$. Then what is the distribution of $X$? Here we need the most important theorem in our entire course: the central limit theorem developed by the French mathematician Pierre-Simon Laplace. The exact proof of this theorem is beyond the scope of this course, so we are just going to use it as a fact. The theorem tells us that provided that the sample size ($n$) is large enough, the sampling distribution of the sample mean follows a normal distribution, even if the population distribution is not normal. More precisely, if $X_1, X_2, \cdots, X_{n-1}, X_n$ are a random sample from a population with mean $\mu$ and variance $\sigma^2$, the sample mean $\bar{X}$ follows a normal distribution
$$\bar{X}\ \dot\sim \ \mathcal{N}(\mu_{\bar{X}}, \sigma_{\bar{X}}^2), \textmd{ where } \mu_{\bar{X}}=\mu, \sigma_{\bar{X}}^2 = \cfrac{\sigma^2}{n}$$
provided that $n$ is large enough. This is a very powerful theorem that allows us making inferences about the population mean using only one sample. We can see that Question Q can be answered by using this theorem.
Now how large is “large enough”? It depends on the population distribution. If the population follows a normal distribution, then $n=2$ is large enough. Otherwise, we may need larger $n$. In general, people tend to think $n \geqslant 30$ is large enough, which seems to work in practice.