With all the examples we have gone through, you can see that we always set the significance level $\alpha$ to be a very small number, with $0.05$ being the most frequently used one.However, it is never 0. The consequence is that there is still a chance we could draw the wrong conclusion when we make a decision based on the p-value. When that occurs, we make errors.
Whenever we make a decision, there are only two possible outcomes: either we reject $H_0$ or we do not reject $H_0$. The ground truth (population), though not known to us, also only has two possibilities: either $H_0$ is true or $H_0$ is false. Therefore, we can have four possible scenario when making a decision after performing a hypothesis testing. You can relate this to the diagnostic testing we talked about in Lectures 5, 6 and 7:
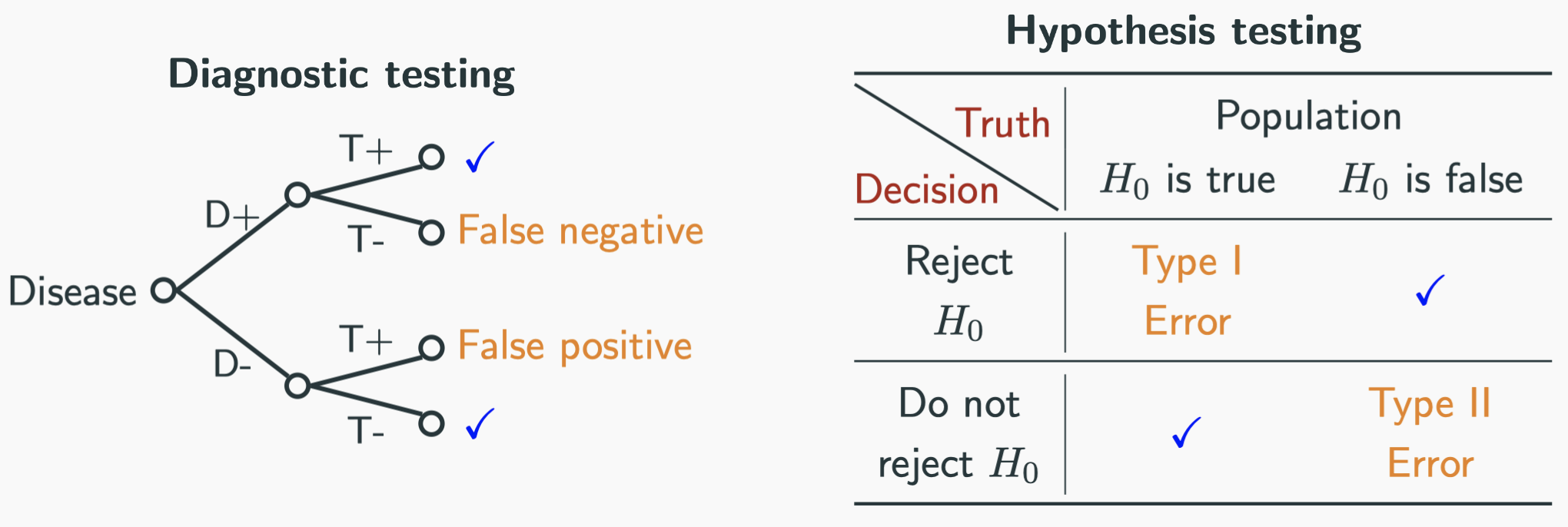
As you can see, in two out of four scenarios, we make mistakes. Statisticians are apparently not good at naming things. The errors are simply named type I error and type II error. You just need to remember them.
In this lecture, we talk about how to analysis the errors, the relationship between them and the sample size estimation.